how to find a limit

Find Limits of Functions in Calculus

Find the limits of various functions using different methods. Several Examples with detailed solutions are presented. More exercises with answers are at the end of this page.

Examples with Detailed Solutions

Example 1

Find the limit

Solution to Example 1:
Note that we are looking for the limit as x approaches 1 from the left ( x → 1^-1 means x approaches 1 by values smaller than 1). Hence
x < 1
x - 1 < 0
If x - 1 < 0 then
| x - 1 | = - (x - 1)
Substitute | x - 1 | by - (x - 1), factor the numerator to write the limit as follows

Simplify to obtain

Example 2

Find the limit

\lim_{x\to\5} \dfrac{x^2-5}{x^2+x-30}

Solution to Example 2:
Although the limit in question is the ratio of two polynomials, x = 5 makes both the numerator and denominator equal to zero. We need to factor both numerator and denominator as shown below.

= \lim_{x\to\5} \dfrac{(x-5)(x+5)}{(x-5)(x+6)}

Simplify to obtain

= \lim_{x\to\5} \dfrac{(x+5)}{(x+6)} = \dfrac{10}{11}

Example 3

Calculate the limit

Solution to Example 3:
We need to look at the limit from the left of 2 and the limit from the right of 2. As x approaches 2 from the left x - 2 < 0 hence
|x - 2| = - (x - 2)
Substitute to obtain the limit from the left of 2 as follows

limit solution to example 3, smaller values

= - 8

As x approaches 2 from the right x - 2 > 0 hence
|x - 2| = x - 2
Substitute to obtain the limit from the right of 2 as follows

final limit solution to example 3, larger values

= 8

The limit from the right of 2 and the limit from the left of 2 are not equal therefore the given limit DOES NOT EXIST.

Example 4

Calculate the limit

Solution to Example 4:
As x approaches -1, cube root x + 1 approaches 0 and ln (x+1) approaches - infinity hence an indeterminate form 0 . infinity

Let us rewrite the limit so that it is of the infinity/infinity indeterminate form.

limit solution to example 4, second step

We now use L'hopital's Rule and find the limit.

Example 5

Find the limit

Solution to Example 5:
As x gets larger x + 1 gets larger and e^(1/(x+1)-1) approaches 0 hence an indeterminate form infinity.0

Let us rewrite the limit so that it is of the 0/0 indeterminate form.

limit solution to example 5, second step

Apply the l'hopital's theorem to find the limit.

= - 1

Example 6

Find the limit

Solution to Example 6:

As x approaches 9, both numerator and denominator approach 0. Multiply both numerator and denominator by the conjugate of the numerator.

Expand and simplify.

limit solution to example 6, second step

and now find the limit.

= 1 / 6

Example 7

Find the limit

Solution to Example 7:
The range of the cosine function is.
-1 <= cos x <= 1
Divide all terms of the above inequality by x, for x positive.
-1 / x <= cos x / x <= 1 / x
Now as x takes larger values without bound (+infinity) both -1 / x and 1 / x approaches 0. Hence by the squeezing theorem the above limit is given by

Example 8

Find the limit

Solution to Example 8:
As t approaches 0, both the numerator and denominator approach 0 and we have the 0 / 0 indeterminate form. Hence the l'hopital theorem is used to calculate the above limit as follows

Example 9

Find the limit

Solution to Example 9:
We first factor out 16 x² under the square root of the denominator and take out of the square root and rewrite the limit as

Since x approaches larger positive values (infinity) | x | = x. Simplify and find the limt.

limit solution to example 9, second step

= 3 / 4

Example 10

Find the limit

Solution to Example 10:
As x approaches 2 from the left then x - 2 approaches 0 from the left or x - 2 < 0. The numerator approaches 5 and the denominator approaches 0 from the left hence the limit is given by

Example 11

Find the limit

Solution to Example 11:
Factor x² in the denominator and simplify.

As x takes large values (infinity), the terms 2/x and 1/x² approaches 0 hence the limit is

= 3 / 4

Example 12

Find the limit

Solution to Example 12:
Factor x² in the numerator and denominator and simplify.

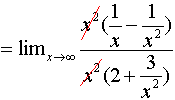
As x takes large values (infinity), the terms 1/x and 1/x² and 3/x² approaches 0 hence the limit is

= 0 / 2 = 0

Example 13

Find the limit

Solution to Example 13:
Multiply numerator and denominator by 3t.

Use limit properties and theorems to rewrite the above limit as the product of two limits and a constant.

We now calculate the first limit by letting T = 3t and noting that when t approaches 0 so does T. We also use the fact that sin T / T approaches 1 when T approaches 0. Hence

The second limit is easily calculated as follows

The final value of the given limit is

Example 14

Find the limit

Solution to Example 14:
Factor x² inside the square root and use the fact that sqrt(x²) = | x |.

Since x takes large values (infinity) then | x | = x. Hence the indeterminate form

Multiply numerator and denominator by the conjugate and simplify

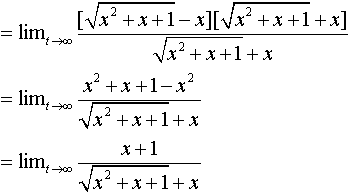
Factor x out of the numerator and denominator and simplify

As x gets larger, the terms 1/x and 1/x² approach zero and the limit is

= 1 / 2

Example 15

Find the limit

Solution to Example 15:
Let z = 1 / x so that as x get large x approaches 0. Substitute and calculate the limit as follows.

Exercises

Calculate the following limits
1)
Calculate limit question 1
2)
Calculate limit question 2
3)
Calculate limit question 3
4)
Calculate limit question 4
5)
Calculate limit question 5
6)
Calculate limit question 6